Der Satz des Thales sagt aus, dass jedes Dreieck, welches auf dem Thaleskreis liegt rechtwinklig ist. Behaupten kann man bekanntlich viel, deswegen muss man solche mathematischen Sätze auch beweisen. Hier nun eine ausführliche Anleitung und Erklärung, wie sich der Satz des Thales Beweis aussieht.
Satz des Thales Beweis Voraussetzungen
Der ursprüngliche Beweis für den Satz des Thales stammt aus der Feder Euklids. Er war ebenfalls griechischer Gelehrter und musste dafür auf ältere bekannte Tatsachen die für alle Dreiecke gelten zurückgreifen.
Die beiden Voraussetzungen für den Beweis nach Euklid ist das Wissen, dass:
- alle Dreiecke eine Winkelsumme von 180° besitzen
– zählt man alle Winkel zusammen muss man auf 180° kommen, ansonsten ist es kein Dreieck! - gleichschenklige Dreieckegleiche Basiswinkel besitzen
– gleichschenklig bedeutet, dass zwei Seiten eines Dreiecks gleich lang sind und solche Dreiecke haben immer zwei Winkel, die gleich groß sind
Wenn man diese beiden Tatsachen kennt, weiß man auch schon alles, was man zum Beweis des Thalessatz benötigt.
Beweis Satz des Thales mathematisch
Durch Konstruktion zweier gleichschenkliger Dreiecke aus dem Ursprungsdreieck ergeben sich die Winkel α und β, sowie γ =α+β
Die Winkelsumme beträgt in einem Dreieck 180°, also γ+α+β = 180°
Nun ersetzen wir γ durch α+β in der Formel und erhalten α+β+α+β = 180°
Fässt man die linke Seite der Formel zusammen lautet diese: 2(α+β) = 180°
Durch eine Teilung durch 2 erhält man das Ergebnis: α+β = 90°
Da wir wissen, dass α+β auch der Winkel bei C ist, muss zwangsläufig jedes Dreieck auf dem Thaleskreis bei γ einen rechten Winkel besitzen.
Beweis Satz des Thales – grafisch
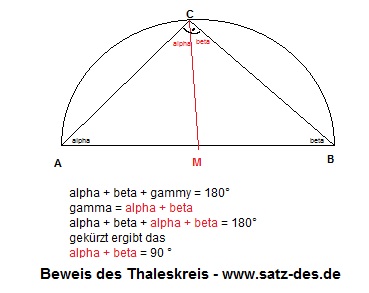
grafischer Beweis Satz des Thales
Wir haben nun ein ganz normales Dreieck nach dem Satz des Thales konstruiert und schauen uns einmal an, was wir damit anstellen können. Wenn wir den Mittelpunkt des Thaleskreises M und unsere Spitze des Dreiecks C mittels einer Linie verbinden, erhalten wir statt einem Dreick zwei Dreiecke. Soweit ist es noch keine Hexerei, aber wir wissen an dieser Stelle schon eine ganze Menge über die beiden neu entstandenen Dreiecke:
Die neu entstandenen Dreiecke sind beide gleichschenklig!
Alle Punkte unseres ersten Dreiecks A, B und C liegen auf dem Thaleskreis und haben somit den gleichen Abstand zu unserem Mittelpunkt M, das heißt A ist soweit von M weg, wie C von M weg ist. Da unsere neuen Dreiecke jetzt die Seitenlängen A bis M, C bis M und das andere B bis M und C bis M haben, müssen sie gleichschenklig sein. Bedeutet, sie haben zwei gleich lange Seiten.
Laut den Voraussetzungen wissen wir schon, dass gleichschenklige Dreiecke zwei gleiche Winkel haben und können diese als α und β einzeichnen. Jetzt haben wir also in unserem Bild vier Winkel eingezeichnet, ohne dass wir etwas vermessen haben oder etwas rechnen musste.
Die andere Voraussetzung mit der Winkelsumme von 180° bringt uns nun den entscheidenden Beweis für den Satz des Thales, da wir ja um auf 180° zu kommen alle Winkel des ursprünglichen Dreiecks zusammen zählen müssen. Abgelesen sieht es dann so aus: α (Winkel bei A) +α und β (Winkel bei C) + β ergeben zusammen 180° des großen Dreiecks. Da der Winkel bei C aus α und β besteht, muss er hier 90° ergeben, da die Figur sonst kein Dreieck sein kann. Es handelt sich hierbei um den selben Beweis, wie er oben schon schriftlich dasteht.