In diesem Beitrag wird die Lösung für die Textaufgabe 4 bei Satz des Thales Rechenaufgaben gezeigt. Die ursprüngliche Aufgabe lautete:
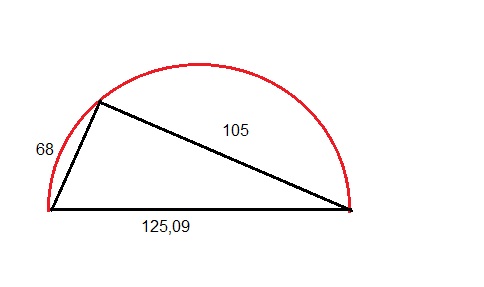
Ulla und Ulf stehen an der Eckfahne am Fußballplatz und wetten, wer schneller an der gegenüberliegenden Eckfahne ankommt. Ulla geht dabei an der Außenlinie entlang (Torseite 68 Meter, Seitenlinie unbekannt) und Ulf diagonal über den Platz und zwar 125,09 m. Wer von beiden ist schneller? Wie lang ist die Seitenlinie? Kann man hier den Satz des Thales anwenden?
Satz des Thales Aufgabe 4 Lösung
Um zur Lösung zu kommen, gibt es verschiedene Möglichkeiten. Einerseits kann man die Aufgabe grafisch lösen, indem man eine Maßstabsgetreue Zeichnung anfertigt.
Wir sehen, dass Ulf definitiv viel kürzer laufen muss, wie Ulla. Man beginnt mit dem Zeichnen der diagonalen Laufstrecke von Ulf, danach sucht man den Mittelpunkt M und zeichnet den Thaleskreis ein (hier rot). Nun kann man an einem Ende der Strecke die 68 m einzeichnen und erhält so die fehlende Grundlinie.
Der zweite Ansatz benutzt im Gegensatz zur grafischen Lösung reine Mathematik und rechnet die fehlende Distanz mittels Satz des Pythagoras aus.
Hierfür verwenden wir die Formel:
a²+b²=c²
nach einer Umstellung erhalten wir die Formel √(c²-a²)=b
Mit den eingesetzten Strecken, die wir aus der Aufgabe kennen ergibt sich folgendes Ergebnis:
√(125,09²-68²)=105 m
Die Seitenlinie beträgt also 105 Meter und Ulla ist somit länger unterwegs als Ulf, da sie 105m + 68m laufen muss.
Der Thalessatz dient hier zur grafischen Darstellung des Problems und zur Konstruktion des Dreiecks.
Mit folgendem Link geht es zurück zu den Rechenaufgaben mit dem Themengebiet Satz des Thales.