Der Satz des Euklid lässt zusätzliche Berechnungen unter Einbeziehung der Höhe und gewisser Hypotenusenabschnitte im rechtwinkligen Dreieck zu. In diesem Beweis verwenden wir das in der Abbildung dargestellte normale rechtwinklige Dreieck ABC mit den dazugehörigen Bezeichnungen.
Höhensatz und Kathetensatz des Euklid Beweis
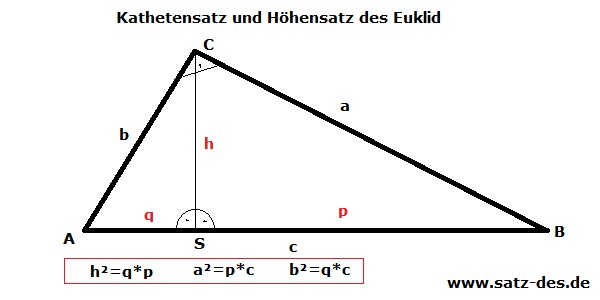
Standard-Dreieck ABC
Wie man sieht, schneidet die Höhe (h) das rechtwinklige Dreieck in der Hypotenuse und formt so zwei weitere rechtwinklige Dreiecke. Dies sind einmal CSB und ASC.
Der Satz des Pythagoras lautet: a²+b²=c²
In diese Formel können wir nun unsere Erkenntnisse und Teilstrecken eintragen, denn hier gilt für a²=p²+h² sowie b²=q²+h² und es gilt c²=(p+q)²
Eingesetzt lautet die gesamte Formel:
(p²+h²)+{q²+h²)=(p+q)²
ausgeschrieben ergibt sich daraus:
p²+2h²+q²=q²+2qp+p² | <<– an dieser Stelle rechnen wir -q² und -p²
2h²=2qp | nun noch :2
h²=q*p
Somit ist der Höhensatz des Euklid bewiesen.
Beweis Kathetensatz des Euklid
Wir beziehen uns wieder auf das oben angegebene Dreieck und rechnen wieder mit dem Satz des Pythagoras. Die korrekte Formel zur Berechnung von b lautet folglich:
a²=p²+h²
Wir wissen nun schon vom Höhensatz des Euklid, dass h²=p*q ist und setzen dies in die Formel ein.
a²=p²+p*q |Nun klammern wir p aus
a²= p*(p+q) | an dieser Stelle sehen wir p+q und dies entspricht der Länge c
a²=p*c
Entsprechend funktioniert dieser Beweis auch mit der Kathete b.